Working backward like cops at a crime scene, Karen Willcox and a team of other engineers and applied mathematicians start with the circumstances and must find the cause – a particular set of parameters. But just as a crime may have many suspects who fit a description, reverse engineering by the numbers may uncover many combinations of parameters that fit the resulting data. Inside these parameters, there’s a lot of room for uncertainty.
Willcox, associate professor of aeronautics and astronautics at the Massachusetts Institute of Technology, and colleagues must compute how certain they are that a specific combination of parameters is the right one. Put in mathematical terms, they are investigating mathematical methods for large-scale statistical inverse problems and uncertainty quantification.
Willcox co-leads a project called SAGUARO that will put these methods to the test. It stands for Scalable Algorithms for Groundwater Uncertainty Analysis and Robust Optimization and is supported by the Department of Energy’s Office of Advanced Scientific Computing Research (ASCR), in the DOE’s Office of Science.
In early May, SAGUARO team members will travel to Berkeley, Calif., to report on their project to other ASCR Applied Mathematics Research investigators from national laboratories and academic institutions.
Inverse problems track back to infer what parameters generated a result. Uncertainty quantification puts a number on the degree to which those calculations can be trusted.
“It’s just a horribly, horribly complicated thing to do,” Willcox says. “It’s funny. People think computers are so powerful these days that we can basically solve any problem. That’s just not the case.”
Solving a “forward problem,” in which the parameters are known and the outcome is calculated, is difficult enough, she says. Turning it around to an inverse problem – while also quantifying uncertainty – creates an almost impossible calculation.
And the more parameters there are to account for, the harder it gets. For the mathematical techniques she investigates, the state of the art is a couple hundred. “When you start getting up to 300, 400 parameters, it’s just very hard to explore that high-dimensional space – and we’re looking at problems where we would like to get up to thousands and even more parameters.”
How contaminants move and react in groundwater is of deep interest to DOE and is a natural inverse problem – conditions underground are largely unknown, and contaminant movement is driven by multiple processes and occurs over a range of time and space scales.
Inverse problem-solving and other techniques the team develops and shares with others could help DOE tackle a range of problems, including managing nuclear waste, sequestering carbon dioxide from power plants and recovering difficult-to-reach oil deposits.
The work is a prime example of how ASCR’s Applied Mathematics Research program plays a fundamental role in helping meet these and many other challenges that are critical to the nation’s future.
‘Often you can find 10 to 30 years of development in an area that has had clear, broad impact and affects the way we do research in the modern world.’
At its basic level, Applied Mathematics Research develops techniques that turn the world into numbers. It states physical processes as discrete equations computers can solve. Applied mathematicians create the nuts and bolts of computer modeling – the fundamental mechanics that make software and simulations on high-performance computers work. No applied mathematicians, no models and no predictive science.
“It’s advanced technology that basically becomes invisible by the time it shows up in applications,” says David L. Brown, deputy director for science and technology in the Computation Directorate at Lawrence Livermore National Laboratory and chairman of a DOE-convened applied mathematics panel that issued a seminal report. “It’s the inner workings that make (computations) faster and more accurate – or in many cases even make them possible.”
Besides subsurface flow, the panel report, “Applied Mathematics at the U.S. Department of Energy: Past, Present and a View to the Future,” outlines other issues important to maintaining and improving the United States’ economic and environmental security:
- Developing technology to make clean coal, next-generation nuclear and fusion power possible.
- Predicting the rate of climate change and understanding those predictions’ accuracy.
- Designing microbes to produce biochemicals, including fuel.
- Increasing the reliability and security of the nation’s power grid.
- Designing and predicting the qualities of nanoscale materials, such as high-temperature superconductors.
- Continuing to ensure the nation’s nuclear arsenal is safe and reliable while guarding against the proliferation of nuclear materials.
Each of these challenges involves complex systems. Simple models and approximations aren’t good enough to provide the science-based information necessary to make sound decisions. Researchers must model these systems across multiple time and space scales and must understand the combinations of processes behind this complexity while calculating the inherent model uncertainties and solution risks.
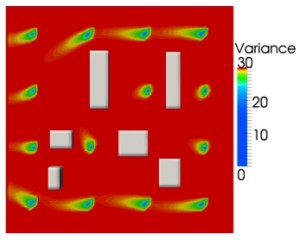
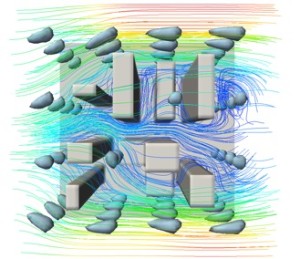
This visualizes a solution of the statistical inverse problem of the contaminant spread, showing the variance in its initial concentration. At left is a cross-section of the variance field through the top row of sensors, with the least uncertainty in the inverse solution near the sensors. The image at right shows isocontours of the variance field superposed on streamlines of the velocity field, which are colored by magnitude.
Computational scientists have two advantages in tackling the task, Brown says. One is bigger and faster machines. “But the other equally important thing is the development of algorithms that will work on those machines and are scalable” – able to run efficiently as the number of processors or the complexity of the architecture in a computer increases. “There’s a lot of mathematics involved in figuring out how to do that.”
Indeed, it would have been impossible to capitalize on the exponential increase in supercomputer speed – from a scale of trillions of operations per second five years ago to quadrillions today – without algorithms developed through Applied Mathematics Research.
Legendary mathematician John von Neumann recognized this link in the 1950s. As a member of the Atomic Energy Commission, an ancestor of today’s DOE, he asked a computer scientist to establish an applied mathematics program at the nascent Los Alamos research facility. That has blossomed into a multifaceted enterprise responsible for the fundamental mathematics that have fueled discovery in a host of disciplines.
For example, the computational fluid dynamics codes used today in aircraft and automobile design, climate modeling, combustion research and other areas are founded in Applied Mathematics research that dates to the middle of the last century. That work also contributed to adaptive mesh refinement (AMR), a technique that makes maximal use of computational power by focusing calculations on the most critical areas of a simulation. The widely used tool was developed through collaborations involving the DOE national laboratories, Stanford University and the Courant Institute of Mathematical Sciences starting in the early 1980s.
The Applied Mathematics program also supported fundamental developments in methods to solve optimization problems, which seek to minimize or maximize a mathematical function. Optimization is used to find the most efficient locations for sensors in a network, ways to distribute power effectively and means to understand reactions behind biological behavior.
Better living through math
The work of applied mathematicians has contributed to meeting national goals and bettering Americans’ lives – improving cars, planes, weather forecasts and climate models; ensuring the security and reliability of the nation’s nuclear deterrent; and making power plants and communications networks more efficient and dependable.
“Often you can find 10 to 30 years of development in an area that has had clear, broad impact and affects the way we do research in the modern world,” Brown says.
The panel Brown headed in 2007 identified three major research areas that capitalize on the Applied Mathematics Research program’s strengths but also address weaknesses in methods for modeling, analyzing and understanding complex systems:
- Predictive modeling and simulation of complex systems, or making models and simulations more accurate, predictable and sophisticated, capable of spanning large scales of time and space and combining many kinds of physics;
- Analyzing complex-systems behavior, or developing approaches that encompass entire systems and processes, such as fusion reactors and carbon sequestration;
- Using complex systems to inform policy-making. If policy-makers are to rely on simulations, then applied mathematics also must quantify the risks behind different courses and the uncertainty underlying the results. Research can help them decide which solutions could be most effective and efficient.
Applied mathematicians not only must tackle these issues and others, Brown says, but also figure out how to do it on computer architectures that continue to evolve. “Put all that together and it’s an enormous challenge for the Applied Mathematics program,” he adds.
Meeting that challenge also will require a different approach to managing the program, the panelists said, and it laid out recommendations to supercharge innovation and discovery.
They advise doing more to encourage and reward risk-taking efforts that lead to breakthroughs. Researchers fear losing funding if they must produce results on a set schedule, making them less likely to take chances. Although oversight is appropriate, the panel suggested there’s a tradeoff between accountability and flexibility.
“Breakthrough discoveries often are made by accident,” Brown says. “Our argument was the best thing to do is to provide a way of supporting our best researchers so they don’t have to risk their livelihoods” when they take less predictable approaches.
The panelists also recommend building effective connections between applied mathematicians and scientists and engineers. They say Applied Mathematics Research yields a greater, faster payoff when its investigators work closely with those who will put their algorithms and codes to work.
Brown and colleagues encourage collaborations between national laboratories and universities in multidisciplinary activities that combine the labs’ aptitude for large-scale, long-term efforts with universities’ self-contained, shorter-term efforts.
And they recommend connecting applied mathematics and advanced computing. Applied Mathematics Research discoveries must be implemented in codes that underpin large-scale models for high-performance computers.
That pairing is yielding results, Brown says. “In many fields, large-scale calculations are really providing scientific insight. Scientists and engineers are starting to make discoveries through computation.”
As predictive science becomes more common, it will increasingly inform policy development in DOE and the U.S. government.
“We face many national and international challenges in which, to develop rational policy, you need to understand scientific facts or at least to understand the ‘what ifs,’” Brown says. Applied Mathematics Research can help supply those facts and portray those scenarios, he adds, by grounding physical abstractions in algorithms that can illuminate complex phenomena and systems.
The DOE Applied Mathematics Research program is a critical component of this country’s technological edge, Brown says. “Losing it would have a long-term detrimental effect on this nation’s ability to compete in the high-tech science-based world.”
“What is important is what it would mean long-term for scientific simulation and ultimately for the DOE and the country. It would be less likely that you’d have developments being made in applied mathematics that would clearly translate into improved capabilities for the U.S. Department of Energy, and hence the country and the world.”
