Making certain about uncertainty
People may dislike uncertainty, Karen Willcox says, but they’d better understand it when making decisions- especially ones affecting millions of dollars and people.
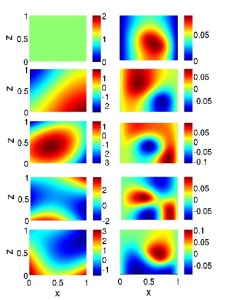
Model reduction approaches the SAGUARO team is developing include simultaneous reduction of the state and parameter spaces. In this subsurface flow application the researchers plotted five orthogonalized basis vectors for the hydraulic conductivity parameter (left) and pressure head state (right). These basis vectors are computed using a sampling algorithm combined with the proper orthogonal decomposition. Visualization by Chad Lieberman, Massachusetts Institute of Technology.
Willcox is part of a team that’s tackling uncertainty in computer models of complex systems like those the Department of Energy must understand to address climate change, groundwater contamination, clean energy and other issues. She and colleagues George Biros of the Georgia Institute of Technology, Clint Dawson and Omar Ghattas of the University of Texas at Austin, and Youssef Marzouk of MIT call their project SAGUARO, for Scalable Algorithms for Groundwater Uncertainty Analysis and Robust Optimization. It’s designed to investigate mathematical methods to sort out uncertainty in these models.“Bringing uncertainty into the decision-making process is difficult, but it’s critically important,” says Willcox, an associate professor of aeronautics and astronautics at the Massachusetts Institute of Technology. That’s especially true of uncertainty in computer simulations, which today play an ever-larger role as officials make policy and chart the nation’s future.
The researchers will tackle inverse problems that characterize subsurface reacting flows and transport – the spread of contaminants in groundwater, the movement of sequestered carbon dioxide and other underground phenomena. It’s one fundamental research area DOE’s Applied Mathematics Research program is concentrating on as it helps tackle some of the country’s most daunting problems.
Although modeling subsurface flows is important to DOE, Willcox says, this class of problems also presents important mathematical challenges. “Many of the different characteristics you would like your methods to handle, subsurface flows have that.”
Yet there are enough similarities to other problems that the techniques the researchers develop will have broad applicability. Those problems typically share the “curse of dimensionality.” In an inverse problem, researchers start with measurements or observations and try to calculate what parameters produced them. But the size of the problem grows exponentially with the dimensionality – the number of parameters. That’s because every added parameter could act with others in any number of combinations to produce the observed result.
The curse of dimensionality makes inverse problems computationally intractable, unless mathematicians find smart ways to sift the dimensions down to only those likely to influence the results. Since many combinations of parameters can fit with the observed results, mathematicians also must assess each to determine the probability it’s the right one.
Willcox and her colleagues use Bayesian inference to get a statistical determination of parameters consistent with the observations. Bayesian methods make a prediction about the probability a hypothesis is true, then repeatedly update that probability distribution as more data come in. Since the distributions reflect confidence in the input values, the method also lets mathematicians quantify uncertainty in the results.
But Bayesian inference poses its own challenges. To arrive at probabilistic predictions that aid decision-making under uncertainty, mathematicians must sample the distributions, then use each sample of parameters in full physics-based models. For complex models with many dimensions, computing these models also can demand huge computer power and time. Mathematicians must find sampling techniques that are faster and more efficient than random.
In other words, Willcox says, the goal is not just to reduce dimensionality, but also to reduce the cost of each point that’s sampled.
The researchers are exploring four methods to reduce complexity. The first is reduced-order modeling, one of Willcox’s specialties. The researchers use mathematical techniques to find a simpler model embedded in the large, complex model that “still represents the physics in a way we want, but is faster to solve,” Willcox says.
Second is using stochastic spectral methods, which approximate the model’s dependence on uncertain parameters, to reduce the complexity of the problem embedded in the Bayesian form.
The third and fourth approaches share some qualities, Willcox says. They attempt to use information from the model physics to drive sampling of the probability distribution. “In classical Bayesian formulations, the physics don’t really inform the way sampling is done.”
The researchers hope the methods they’re testing will guide sampling in a smart way, based on details from the problem’s structure, such as derivative and Hessian information.
The model reduction and stochastic spectral methods are different yet complementary ways to reduce complexity of the statistical inverse problem, the researchers say. They plan to compare them and find ways to combine aspects of each.