Electrons – small, charged and abundant – complicate materials science simulations. Because their effects often are tiny and the cost of considering them in calculations is high, researchers often ignore them for practical reasons. If their effect is negligible, leaving them out gives scientists reliable answers quickly and efficiently.
But sometimes ignoring electrons isn’t possible. In strongly correlated materials – a class that includes superconductors, magnets, quantum spin liquids and more – electron interactions are significant and critically important. In these materials, Coulomb interactions – the attraction between oppositely charged particles and the repulsion between similarly charged ones – nearly match the kinetic energy or other physical properties. The compound doesn’t know what it should optimize, says Thomas Maier of the Department of Energy’s (DOE’s) Oak Ridge National Laboratory. “These materials have many different phases of phenomena,” such as magnetism or superconductivity. “But that’s what makes them interesting because you can then think about tuning the system from one state to another state, such as between a magnet and a superconductor, by just changing something as simple as pressure.”
Some of these materials, such as high temperature superconductors and quantum spin liquids, hold promise for energy transmission, sophisticated magnetic devices for science and quantum computers. But to pursue this technology, researchers must first better understand the compounds’ mysterious behavior. Maier and his colleagues have used awards of computing time from the DOE’s INCITE (Innovative and Novel Computational Impact on Theory and Experiment) program to model the physical theory that underpins this complex behavior.
Superconductivity, which allows electricity to flow unimpeded through materials, was discovered more than a hundred years ago. But the idea was mostly impractical: To acquire the desired property, these initial materials – now known as low-temperature, or conventional, superconductors – had to be cooled to near absolute zero (0 degrees Kelvin) with expensive liquid helium. In 1986, however, researchers discovered high-temperature, or nonconventional, superconductors, a different material class that exhibits this sought-after phenomenon at around 100 degrees Kelvin. Because of this higher transition temperature, such compounds can be cooled with liquid nitrogen, a cheaper and more available alternative to helium.
But even after 30 years, scientists are still trying to piece together exactly how high-temperature superconductivity works. Although the normal state of conventional superconductors can be understood through single-particle theory, physicists need many-body theory – which considers how at least some of the individual electrons behave separately – to describe high-temperature superconductors. Such calculations are difficult and computationally expensive.
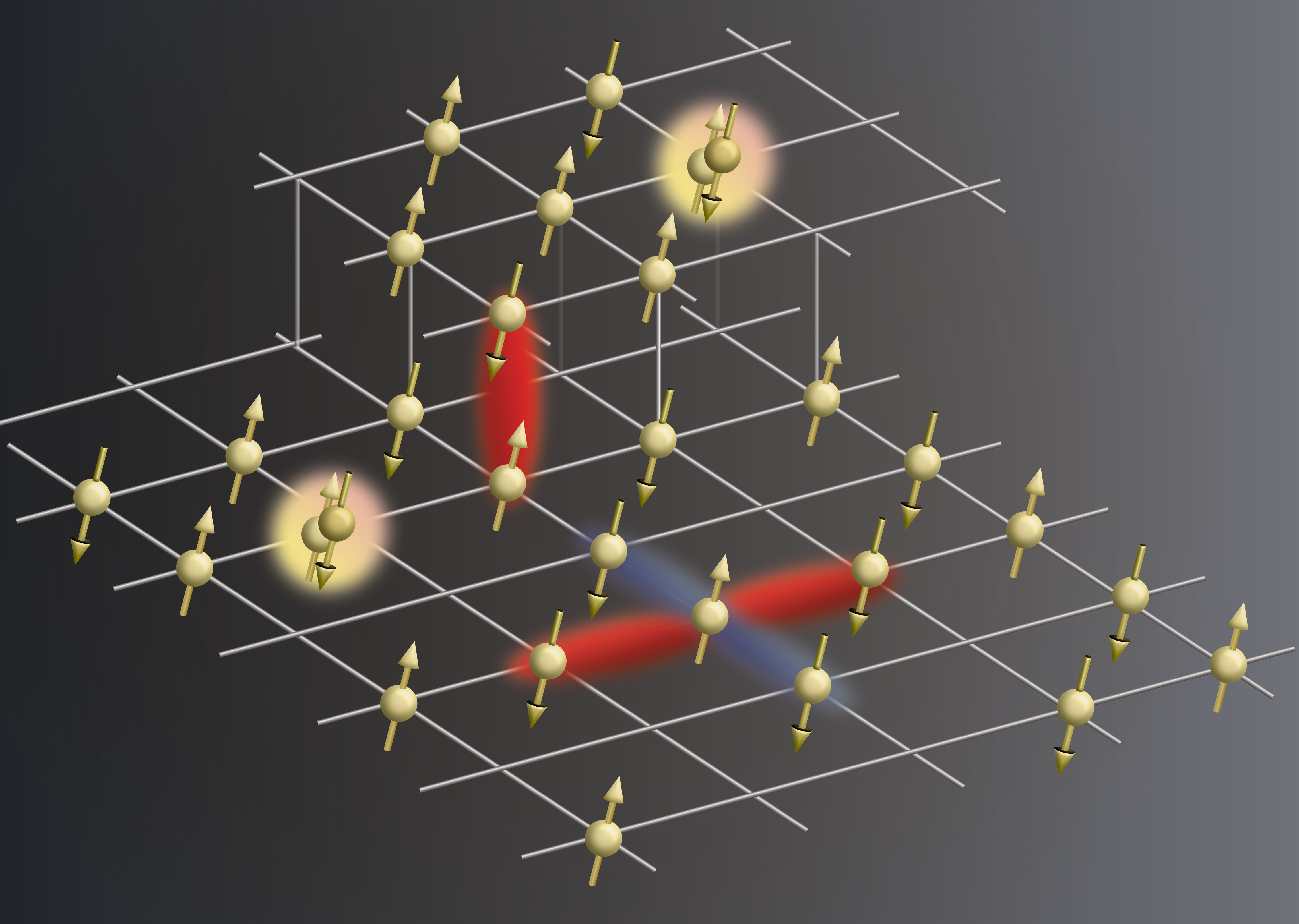
Maier and his colleagues use the two-dimensional Hubbard model, which relies on theory widely believed to include nonconventional superconductivity’s key components. So far, the team has primarily used a two-dimensional one-band model that describes a single orbital per atom where up to two electrons can reside – a small subset of a compound’s total electrons. “It sounds very simple,” Maier says, “but the physics is very rich.”
Cooper pairs moving in sync is a hallmark of superconductivity.
With the simplified Hubbard model, researchers can observe puddles of high electron density; regions with few electrons; electron patterns that form sinusoidal waves; how electrons align their spins, which makes materials magnetic; and, not least, how electrons couple at low temperatures to form Cooper pairs, neighboring boson-like duos. Bosons are one of two main classes of particles, and more than one can exist in the same quantum state. Free electrons are fermions, the other particle type, which cannot exist in the same quantum state. Cooper pairs moving in sync is a hallmark of superconductivity.
Researchers have learned a lot from these models, Maier notes, but their results so far have been qualitative. The 2-D, one-band model provides an approximate transition temperature for these superconductors at 100-degree Kelvin. But transition temperatures observed in related materials can differ, sometimes widely. For example, two different cuprate (copper-containing) superconductors, lanthanum barium copper oxide (LBCO) and mercury thallium barium calcium copper oxide (HgTlBaCaCuO), have transition temperatures more than 100 degrees apart, up to 35 and 150 Kelvin, respectively.
To address those details, Maier and his colleagues are using their most recent INCITE allotment of 900,000 node-hours on Summit, the IBM AC922 system at Oak Ridge National Laboratory, to explore more complex versions than the 2-D one-band Hubbard model. Co-investigators include Satoshi Okamoto, Gonzalo Alvarez and Eduardo D’Azevedo of ORNL; Steven Johnston of the University of Tennessee, Knoxville; Thomas Schulthess of the Swiss National Supercomputing Centre; and Douglas Scalapino of the University of California, Santa Barbara.
A more complex model – the 2-D three-band version – includes three electron types typically found in a high-temperature superconductor for orbitals on copper and oxygen atoms in a cuprate superconductor. To examine another type, iron-based superconductors, they’ll use even more complex models that examine five orbitals on iron atoms. These more complex systems will demand even greater computational power.
Maier and his colleagues also are exploring the physical behavior of quantum spin liquids, unusual magnetic materials with quantum entanglement, in which the state of two particles are linked even over great distances. In these materials Coulomb interactions are strong, and the electrons are incredibly localized, remaining near a single atom. The theory of quantum spin liquids is far less understood than that of superconductors. Electron spins in these materials don’t align at low temperatures. Instead the subatomic particles acquire topological order, a certain pattern of long-range quantum entanglement. When a group of particles is entangled, a single particle’s state can’t be described independently from the others’ state. Under these conditions, electrons can assume different quantum identities, becoming particles, known as non-Abelian anyons or Majorana fermions that could be useful for quantum computers.
The Kitaev model, one possible description for quantum spin liquids, simulates electrons’ behavior in a lattice arrangement. Electrons have two spin states, and they prefer to be arranged next to neighbors with an opposite spin. Some lattices, however, such as the triangles or hexagons proposed for quantum spin liquids, force the electrons into patterns that don’t allow opposite spins for all their neighbors, a situation known as geometric frustration. Instead, the materials may create a topologically ordered state, in which pairs of electron spins are entangled over long distances, and out of which these other, exotic particles can emerge – the non-Abelian anyons and Majorana fermions.
This type of long-range entanglement could be used as a basis for quantum computing materials, but physicists have to understand it first. They also must understand which materials exhibit this complex behavior.
Based on neutron-scattering experiments, researchers think ruthenium trichloride might form quantum spin liquids. Maier and his colleagues are using a version of the Kitaev model to run large-scale simulations of this material’s behavior and comparing the results with experimental data. They want to know whether the Kitaev model is a good one for ruthenium trichloride and to eventually identify other materials with these unique properties.
Getting a better grasp on strongly correlated materials remains one of the most challenging theoretical problems in materials science, Maier says. “The interactions between the electrons are strong,” he adds, and quantum many-body theory is both complicated and numerically expensive. They can’t simultaneously examine 1023 (a 1 with 23 zeroes, or 100 sextillion) electrons. “So what we do in this field is reduce the problem to a more manageable one.”