A Duke University team is learning to track roving killers: tumor cells that separate and circulate through the body before attaching elsewhere and metastasizing, a process behind 90 percent of U.S. cancer deaths.
Oncologists struggle to understand how individual
cells – and, more often, gangs of them – move through the body’s circulatory system as fluid forces toss them and narrow vessels squeeze them.
The researchers are getting help from HARVEY, a full-body model of the human vascular system that has earned honors over the past few years. Now they’re extending that code to characterize properties that influence cancer cells’ treks through blood vessels and where they attach to grow new tumors. The model is named for William Harvey, a 17th century surgeon who described the circulatory system.
The group, led by Amanda Randles, is advancing its search with a Department of Energy (DOE) INCITE (Innovative and Novel Computational Impact on Theory and Experiment) grant of 290,000 node-hours on Summit, an IBM AC922 supercomputer at the Oak Ridge Leadership Computing Facility, a DOE user facility. In a separate project, a HARVEY cancer cell simulation also will be among the first codes to run on Argonne National Laboratory’s Aurora, expected to be one of the nation’s first exascale systems, capable of 1018 scientific calculations per second.
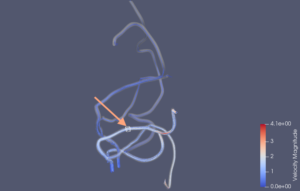
A model convoluted circulatory system with the arrow indicating the location of the multiphysics adaptive moving window seen in the illustration above. The window concentrates computing power to track cells’ movements through the system in high fidelity. Image courtesy of G. Herschlag, J. Gounley, S. Roychowdhury, E. W. Draeger and A. Randles, from “Multi-physics simulations of particle tracking in arterial geometries with a scalable moving window algorithm,” 2019 IEEE International Conference on Cluster Computing (CLUSTER), Albuquerque, NM, USA, 2019, pp. 1-11, doi: 10.1109/CLUSTER.2019.8891041.
Such projects will stretch the limits of biomedicine and computer science, says Randles, a biomedical sciences professor and a 2013 alumna of the DOE Computational Science Graduate Fellowship. Even with full access to Summit or another high-performance computing (HPC) system, it’s impossible to simulate all the individual cells a model would need to account for to be useful. So her lab is developing algorithms that focus computational power where it’s needed most, enabling larger circulatory network simulations that include multiple kinds of physics across varying time and length scales. The INCITE grant “will be our opportunity to really test that out and validate it – really push the models,” she says.
The HARVEY code excels at capturing red blood cell behavior – how they deform and flow. But cancer cells present different modeling challenges. They have nuclei, which blood cells lack, and are larger, ranging from 10 to 20 versus 8 to 10 millionths of a meter across. Cancer cells deform less, form clumps and can stick to blood-vessel walls and other tissues. Her team’s goal is elucidating “the parameters that really describe that specific cell type and how that influences how it’s going to move through different geometry.”
It’s taken Randles’ team two years to develop a model of a single circulating cancer cell and validate it with comparisons to lab experiments. “But there’s a lot of interest in clusters and how they survive” moving through blood vessels of different sizes and shapes “and if you have multiple cancer cells, how they interact,” Randles says. Cells in a clump may be heterogenous, with varying sizes, shapes, deformity and more. “You can see how the parameters explode,” creating a gnarly computational modeling problem.
The general approach is like a moving window that follows cancer cells as they travel through blood vessels.
If Randles and her team succeed, however, their code could manipulate and isolate those factors in ways lab experiments can’t. “The cool thing about computational science is that we can turn on and off specific parameters,” she says. The model can test, for example, how individual changes in the cell nucleus, such as its elasticity, its stiffness or the viscosity of the fluid it contains, affect its trajectory through blood vessels. “We’re isolating how that one tiny variable influences” the cell. “That’s a surprisingly powerful capability,” that can arm oncologists and pharmaceutical researchers in their battle against this indecipherable disease. Knowing which properties influence cell movements could provide drug targets. Identifying how particular tumors sheds cells and where those cells attach could help slow the cancer’s spread.
Reaching that point, however, requires considerable algorithmic innovation. An earlier project with Lawrence Livermore National Laboratory, published in Science Advances in August 2020, helped Randles realize that using brute-force calculations, even with increasing computer power, won’t portray interactions of cancer and blood cells with fluids and arterial structures in sufficient detail to capture behavior the scientists must understand. The team needs methods that use selective approximations to make the problem tractable.
The group still is refining its code, but the general approach is like a moving window that follows cancer cells as they travel through blood vessels, Randles says. Within the window, the algorithm explicitly portrays how individual cancer and red blood cells behave. Outside, the algorithm treats flow through the vessels as a bulk fluid, a less demanding calculation.
“You can imagine all of the challenges in trying to make that work accurately,” Randles says. Inside the window, the grid of points at which the computer calculates physical forces and cell movements is tightly spaced for higher resolution. Outside the window the grid is coarse. “The viscosity of the fluid in the window is different than what’s outside the window,” making it tricky to couple the two into one simulation. It’s also challenging to properly set the simulation’s initial conditions and capture cell deformation. Then there are computer science obstacles like ensuring work is evenly distributed among hundreds of thousands of processors, allocating tasks between standard processors and accelerators, such as graphics processing units, and getting a stable code that converges to a solution.
“Then, assuming you have it converged and you have it all coupled properly, are you actually getting the right value?” Randles says.
One of the first goals for the group’s INCITE allocation will be answering that question. The Duke researchers began working with Jeffrey Vetter’s Oak Ridge National Laboratory group last year, using a lab director’s discretionary allocation to optimize the code for Summit. Now they’re preparing a validation test “so we can trust that this method is accurate and then we can move forward with actually using it,” Randles says.
The test is one of the largest fluid-structure interaction models ever run, Randles says – a brute-force calculation to compare with the team’s selective approximation method. It models every red blood cell in a large, complex vessel network, testing the limits of such a calculation on all of Summit’s 4,608 nodes.
Ultimately, Summit will let Randles and her colleagues refine their model and test specific factors influencing metastasis. It’s important to understand “the interplay between nucleus size, nucleus stiffness, membrane stiffness, all of these different parameters” and how they “come together to determine where the cancer cells actually go.”
With Summit’s power and the group’s new methods, researchers will be able to follow cells longer and through larger and more complex vascular systems than under current models. “We can actually track the cell movement over a useful distance to see where it’s going, what (vessel) branches it’s going to and what factors are driving that,” Randles says, adding “you just couldn’t do that on other (HPC) systems.”
In the long run, Randles and her colleagues want to produce useful software for cancer researchers, even those with limited computer science expertise. “We refer to it as a mini-app, an open-source tool that’s not a full-blown HARVEY” but with similar capabilities. The program could run on computer clusters or in the cloud and would let doctors change parameters and see the effects on cell movement. Ideally, the code could “drop the cell in and give you a basic understanding to mimic your experimental data.”
