When it comes to the power that keeps our lights on, our food cold and our computers and TVs operating, we don’t want to consider the what ifs: What if the power goes out? What if supply can’t keep up with demand?
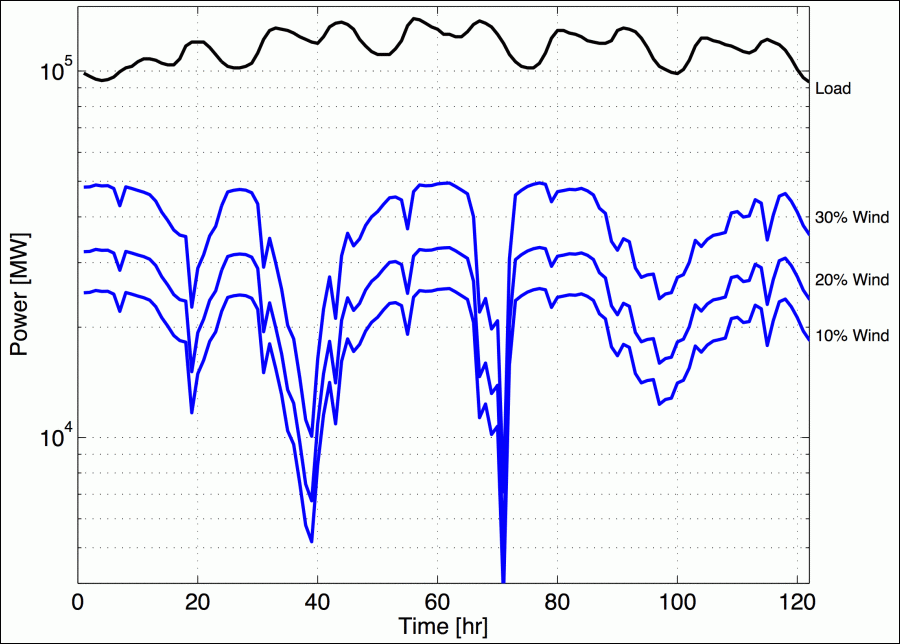
“We all know that once you go into what ifs, it’s a big set of what ifs,” says Mihai Anitescu of Argonne National Laboratory. And uncertainties only multiply as utilities add renewable energy sources such as wind to an already enormous and complex power grid. Each wind turbine increases variability in the power supply. Utilities must address new questions like, What if wind energy suddenly increases in the Chicago area but drops off around St. Louis? What if we count on wind energy but it doesn’t come through?
“Once you go into all these branches, the problem grows big,” Anitescu says – so big that only high-performance computers can provide some answers. The research team he heads designs algorithms computers use to address optimization under uncertainty – a systematic way of asking what if to make the best decisions given randomly changing circumstances.
Anitescu, a computational mathematician at Argonne’s Laboratory for Advanced Numerical Software, builds algorithms with a range of uses. The Multifaceted Mathematics for Complex Energy Systems (M2ACS) project he heads takes a multipronged mathematical approach to operating the best possible power grid in the face of increasing demands and complexity. The project unites scientists from Argonne, Pacific Northwest and Sandia national laboratories and the universities of Wisconsin and Chicago. The team seeks computational ways to address permutations of that fundamental question: What if?
‘You sit down and you contemplate and say, “Boy, life is nice.” I cannot describe it any other way.’
Electricity, as things stand now, can’t be stored on a large scale. Utilities and the regional transmission grids that deliver power over multiple states constantly perform a balancing act, keeping supply roughly in line with demand. Generate too little and you risk brownouts and blackouts. Generate too much and you’re wasting resources and money.
Utilities and grid operators traditionally deal with these what ifs by building in margin: reserves of power generation capacity. “You effectively pay money for a possibility,” Anitescu says. “Maybe that possibility occurs. Maybe it doesn’t.” Renewable resources introduce added possibilities, prompting engineers to build additional conventional power to increase margin. That adds costs and – because most of the extra plants burn gas or coal – pollutants that could offset the environmental benefits of wind or solar.
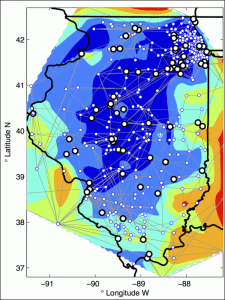
This shows the Illinois power grid system overlaid on fields portraying electricity prices under a deterministic economic dispatch scenario. Dark blue areas have the lowest prices while red and yellow have the highest. Argonne National Laboratory researchers use a model of the Illinois grid to test algorithms for making power dispatch decisions under uncertainty. Credit: Argonne National Laboratory.
Engineers typically determine margin in off-line studies carried out long before grid operators actually dispatch energy to meet demand. “That means (margin) is not set in light of all the available information you have at the time you have to make decisions,” he says, such as how much generation is available at a particular moment. Computation could take that information – about the state of the system, how much renewable power is expected to be available and other conditions – into account when making dispatch decisions. “Then maybe you have less margin. It will cost you less to operate the system.” The goal is to use more renewable energy with the same safety margin and reliability.
Getting there, however, is a huge challenge. First, regulations say grid operators must account for system state and generation capacity (based on demand, weather conditions and other factors) out to at least 24 hours ahead – and update dispatch decisions at least once an hour. “That multiplies your problem by 24, because you have to consider 24 specific time horizons at any time. If I make my decision today, I have to consider the impact it’s going to have all the way to the same time tomorrow.” The problem may only get more difficult. Grid operators and regulators have discussed extending the time horizon to as long as 72 hours and tightening update frequency to less than an hour – perhaps as little as every five minutes, Anitescu says.
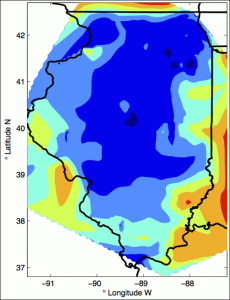
This shows electricity prices in Illinois under a stochastic economic dispatch scenario. The dark blue region, representing areas with the lowest prices, is larger compared with that in the deterministic economic dispatch scenario. Argonne National Laboratory’s simulations show that stochastic dispatch leads to more homogeneous prices and a more even spread of social welfare than the deterministic approach. Credit: Argonne National Laboratory.
Second, the calculations have to represent the entire power network: a giant graph of generators, transmission lines and other facilities, with each part a variable in the calculation. Just in Illinois, where Argonne is based, the grid has thousands of parts – but grids typically are controlled over much larger areas, like the entire Midwest.
“Then, on top of that, you have the number of scenarios you have to consider,” Anitescu says: the thousands of what ifs of wind and solar generation, rising or falling demand and other factors. That grows the problem into billions of variables and constraints, many of which are constantly changing. “Any decision has to have all these variables, and each hour I get new data” on the system’s state. “I put it all in and then I do it again,” solving the problem within an hour to meet the demand for updated dispatch decisions.
Other M2ACS researchers probe state estimation: how data are gathered and analyzed to describe the grid’s condition at any given time. Anitescu and others at Argonne, including scientist Cosmin Petra, work on algorithms for dispatch – the 24-hour merry-go-round of updating power generation decisions based on state estimation data and thousands of scenarios.
To tune and test PIPS, their approach to solving power dispatch problems under uncertainty, Anitescu and Petra used a DOE Innovative and Novel Computational Impact on Theory and Experiment (INCITE) grant of 10 million processor hours on Intrepid, Argonne’s IBM Blue Gene/P. Their goal was to get at or near what’s considered real-time performance in the power industry: a solution in under an hour.
PIPS is similar to most other approaches to optimization under uncertainty, Anitescu says, and much of the solver is comprised of readily available tools. What’s difficult is making those parts work together to attack the problem quickly and efficiently. Programmers must limit communication within a node (a group of processors sharing local memory) and between nodes.
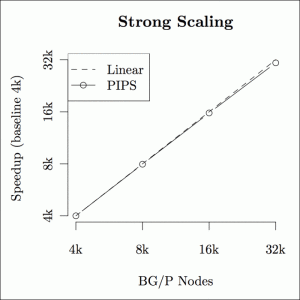
The PIPS solver scaled strongly on a stochastic economic dispatch problem run on Intrepid, Argonne National Laboratory’s IBM Blue Gene/P supercomputer. That means PIPS was proportionally faster as the number of processors it ran on increased, from about 4,000 nodes up to about 32,000 nodes. The dashed line is perfect scaling; the solid line is actual PIPS performance for five iterations. Scaling efficiency ranged from 96 to 99 percent. Credit: Argonne National Laboratory.
With modifications to reduce communication, the researchers found PIPS scaled strongly – it was proportionally faster as the number of processors it ran on increased. Nonetheless, it could still not make power dispatch decisions for the grid covering Illinois with real-time performance. The researchers went back to work, reformulating the way PIPS solves the inner problem on the node to boost its speed by 10 times. PIPS scales at the same rate, Anitescu explains, “but now I’m doing things 10 times faster at any scale.” The result: a solution in under an hour for dispatch decisions out to a time horizon of 12 hours.
It was a culmination of years of research that came before the INCITE grant: setting up the problem, gathering data, modeling the Illinois power network and more. When Anitescu learned in December that the solution finally took under an hour, it was “like happiness flowing through your veins,” he says. “You sit down and you contemplate and say, ‘Boy, life is nice.’ I cannot describe it any other way.”
The pleasure was short-lived, largely because there is still much to do. For one thing, the solution is just for a system the size of Illinois. Anitescu and his colleagues aim to model a full Independent System Operator (ISO) region, a federally established organization that coordinates power distribution through large swaths of the country – the Midwest, for example.
For another, the problem still requires huge computing resources ISOs may not afford. That may change as computers march toward higher performance at lower costs, and with continued research, algorithms could run fast even on smaller computers. And the problem size may shrink, as research finds modeling just a few hundred or a few thousand scenarios is adequate to account for uncertainty, instead of tens of thousands.
With a 2013 INCITE allocation of 14 million processor hours on Intrepid, Anitescu and his colleagues will test PIPS scalability by introducing added details to the problem. The biggest will be power commitment: deciding whether to start a power plant or generator over 24 hours, rather than just adjusting how much power it produces, as dispatch does. “When you combine the yes/no’s in all the possible configurations, you get lots of options,” Anitescu says. This integer variable problem, combined with optimization under uncertainty, is much more difficult to solve.