Part of the Science at the Exascale series.
The periodic table of the elements hanging in most chemistry classrooms has about 100 entries – and is just the first few words in the story of chemical interaction, says James Vary, professor of physics at Iowa State University.
Those entries represent only one form of each element, with a particular number of neutrons and protons, collectively known as nucleons, in the nucleus of the element’s atoms. But “the chart of the atomic nuclei – the isotopes – has thousands of entries since there are a variable number of neutrons for each chemical species,” Vary says.
Many of those thousands of nuclei are unstable and difficult to study experimentally. Nonetheless, they play crucial roles in generating nuclear energy and maintaining national security. Consequently, “we need forefront theoretical calculations to characterize” their properties, Vary says.
For example, nuclear physicists continue to search for the connection between quantum chromodynamics (QCD) – the theory of quarks and gluons – and nuclei. Although QCD is the theory for the strong interactions between particles, such as the nucleons, more work remains to understand how quarks and gluons lead to neutrons and protons or other strongly interacting particles.
“We don’t know the force among protons and neutrons well enough,” says David Dean, who directs the Physics Division at Oak Ridge National Laboratory and has been on special assignment as senior advisor to the under secretary for science at the Department of Energy (DOE). “So we work on various calculations to help us pin down what that force is and how it is acting.”
To search for this force between neutrons and protons, Dean takes a range of approaches. For example, for several years he’s worked on ab initio theories of nuclear structure – theories based on fundamental physics with few assumptions. That work included a grant from INCITE (Innovative and Novel Computational Impact on Theory and Experiment), a DOE program that awards large slices of time on high-performance computers. He’s also used INCITE time to simulate phase transitions in warm, rotating nuclei. “We are working on a paper dealing with the anomalously long lifetime of carbon-14 from an ab initio point of view,” using INCITE time to run applications at petascale – quadrillions of calculations per second.
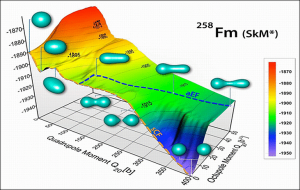
Computation plays a key role in many aspects of nuclear physics. Here, for example, researchers used a standard phenomenological energy-density functional to compute the potential energy surface of fermium 258. In two fission paths shown, the blue figures indicate the evolving shapes. Image courtesy of A. Staszczak, A. Baran, J. Dobaczewski and W. Nazarewicz, Oak Ridge National Laboratory.
Dean and Vary belong to a group of nuclear physicists who, Vary says, are “developing, verifying and validating methods to calculate nuclear structures and nuclear cross-sections that are useful but cannot be measured directly in laboratory experiments.”
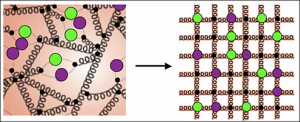
Quantum chromodynamics (QCD) describes interactions between quarks (colored circles) and gluons (spring-like lines) in the image at left. Lattice QCD can be used to solve QCD equations by introducing a numerical grid of space and time (right). Images courtesy of Thomas Luu, Lawrence Livermore National Laboratory, and David Richards, Thomas Jefferson National Accelerator Facility.
Understanding interactions among neutrons and protons will require exascale computers – a new generation of machines about a thousand times faster than those physicists now use to explore nuclear structure. For the thorniest nuclear physics, “the growth of the problem size is combinatorial with the number of particles in the system,” Dean says. Consequently, “you want as big of computer as you can get.”
To solve questions related to QCD, researchers often use lattice QCD (LQCD), solving QCD equations on a numerical grid of space and time.
Emphasizing the importance of LQCD for nuclear physics, David B. Kaplan, professor of physics and director of the Institute for Nuclear Theory at the University of Washington, describes a ladder of computations from light nuclei to heavy. “At the most fundamental level, one would like to derive nuclear properties from the fundamental interactions between quarks and gluons using LQCD. This becomes intractable for any but the lightest few nuclei, but is sufficient in principle to extract the fundamental interactions between nucleons.”
For example, LQCD can compute the energy levels of three neutrons in a box, obtaining information about so-called three-body forces that is inaccessible to experiment. “Currently it’s not a clean extraction,” Kaplan says, “but the desired physics is definitely within reach with the next generation of supercomputers.”
The first-rung interactions can be the input for the next rung on the ladder – solving the many-body Schrödinger equation for nucleons, Kaplan says. “Currently, such Schrödinger equation computations can reach carbon and will perhaps eventually get to calcium before they too become intractable.”
Getting to even heavier nuclei requires different approaches, such as density functional theory (DFT). Here an energy density functional – an integral of a function of particle densities composed of proton and neutron densities, spins, momentum and more – can determine the densities of protons and neutrons that make up even heavy nuclei. Determining the optimal form of the functional will rely heavily on results obtained from LQCD and the Schrödinger equation approach for light and medium nuclei, as well as from experimental data. Some ongoing work in this area, such as the DOE’s Universal Nuclear Energy Density Functional collaboration, is already showing progress with heavier nuclei.
DOE supports a number of LQCD collaborations, including the Nuclear Physics with Lattice QCD collaboration (NPLQCD), which consists of researchers from Indiana University, Lawrence Livermore National Laboratory, the College of William and Mary, the University of Barcelona, the University of New Hampshire and the University of Washington. The NPLQCD aims to use LQCD to calculate the structure and interactions of the lightest nuclei. For example, researchers in this collaboration want to unveil properties and interactions of a deuteron (a single proton and neutron, the nucleus of the hydrogen isotope deuterium) – all directly from QCD. The technology this collaboration is developing will add to the experimental database, says Martin Savage, professor of physics at the University of Washington and NPLQCD group member.
To explore ever-larger simulations, many areas of expertise must be combined. This will include theoretical nuclear physics, computer science, algorithms and more. For example, Kaplan focuses on what he calls “putting physics on a computer” – ways to extract the most physics from a limited computation, with as complete an understanding as possible of errors in the results.
Advances in simulating nuclear physics, using methods such as LQCD and DFT, bring steadily increasing statistical accuracy. For researchers to understand the meaning of their results, however, there must be a corresponding improvement in understanding the systematic errors arising from the underlying assumptions and the computational methods used. Says Kaplan, “This requires a deep understanding of physics, the computer and the algorithms, all at the same time.”
Besides the inner space of nuclei, some simulations reach into outer space. For example, a supernova is born when a massive star burns out. Bright explosions can use up the star’s remaining fuel, leaving its center to collapse, creating incredible densities of nuclear material. This prompts additional scenarios in which researchers can simulate how nuclear matter behaves and interacts.
“We don’t know a lot about densities beyond what you can get on earth,” Savage says, “so there are significant uncertainties when you squeeze nuclear matter. Exascale computing will reduce the uncertainties in our simulations of extreme conditions” – such as matter at extreme pressures and temperatures.
These issues aren’t purely academic. Understanding these processes will go a long way in understanding the synthesis of the universe’s elements – and ultimately life as we know it.
Many of today’s outstanding questions in nuclear science cannot be answered without significant increases in high performance computing resources. In a sense, the problems nuclear physicists look into will always require ever-greater computing capabilities. “Computation is like a gas,” Dean says. “You fill up whatever you have in front of you.”
Plus, what researchers fill up with exceeds the theoretical amount of computer power they have access to. For instance, Savage estimates that of all the petaflops available on high-performance computers, nuclear physics’ share is 20 to 30 teraflops.
Even if nuclear physicists got every flop available, work would still be required in other areas. “To get optimized code that will run on the exascale machines will require lots of effort and expertise from outside the nuclear-physics community,” Savage notes. For instance, physicists will need new applied mathematics developed just for exascale computations.
What’s more, every existing application will need to be scaled up – made to run on an exaflops-capable machine. Though some applications will scale up more easily than others, significant work must be invested in preparing for the next generation of high-performance computing resources. Dean offers an example. “We also use a nonlinear equation approach where we will need to think about how the data are distributed.” For large matrix diagonalization, a linear algebraic method Dean and his colleagues use, scaling up “will take thinking about the algorithms.”
These exascale advances, though, will go beyond theoretical physics and outer space. Improved simulations also will benefit applied research, such as nuclear accelerator design. “By being able to more accurately simulate accelerators,” Savage says, “you will be able to refine the engineering and build the machines for less.”