No one can be quite sure what goes on underground, and that’s largely why brothers Daniel and Alexandre Tartakovsky find the subterranean so fascinating.
Daniel is a professor at the University of California, San Diego, and Alexandre is a scientist at Pacific Northwest National Laboratory. Working with other researchers, they are developing mathematical methods to model subsurface flow and transport and to quantify predictive uncertainty.
Computer models of subsurface flow and transport are important to DOE – and to the United States. Protecting the environment, remediating contaminated sites, enhancing oil and gas recovery and geological carbon dioxide sequestration to slow climate change are just some of the applications requiring such models. The methods the researchers develop also could be used in a range of fields, including nuclear engineering, material science and cellular biology.
Subsurface flow and transport also are good subjects for developing and testing tools that quantify uncertainty in models’ predictions. “Many of the parameters are, in principle, not knowable,” Daniel says. The dearth of data and questions about the validity of mathematical conceptualizations of physical and biochemical subsurface processes contribute to uncertainty.
Uncertainty quantification is one of Daniel’s main interests, whereas Alexandre works more on multiscale methods to describe fluid flow and biochemical processes. The brothers followed the same path, however, to specialize in hydrology and applied mathematics and they collaborate frequently.
Tracking and predicting the migration of contaminants like strontium, neptunium or other contaminants as water carries them in the subsurface is a tricky proposition. “You have your subsurface environment and you are interested in some biological or chemical processes there,” Daniel says. “To model things with certainty one would, in principle, need to know the shape of every pore in a heterogeneous environment that consists of billions upon billions of pores of various sizes and shapes.”
The model is important for devising ways to remediate subsurface contamination, including radionuclides.
Such information is never available, and even if it were modeling processes in those pores would demand tremendous computer power and processor time. To make the problem tractable, researchers commonly average the pore-scale governing equations – including the advection-diffusion equation describing solute transport and the Navier-Stokes equation describing the flow of incompressible fluids – over a large volume of a porous medium.
This gives rise to continuum or macroscopic models that “work fine in most cases, except when they don’t,” Alexandre says. A case in point is reactive transport, which is described by a coupled system of nonlinear differential equations.
Continuum-scale advection-dispersion equations (ADE) combine the effects of mechanical mixing (driven by variations in pore-scale fluid velocity) with diffusion mixing (driven by the Brownian motion of particles). Observations show the two effects are fundamentally different, the Tartakovskys and Paul Meakin of the Idaho National Laboratory demonstrated in a July 2008 paper in Physical Review Letters. Standard ADE-based models, they say, can “significantly over-predict the extent of reaction in mixing-induced” chemical interactions.
The classical models provide an average description of fluid flow and solute transport. “When you average, you are getting a mean behavior, and we found that it’s not enough to calculate complex phenomena such as reactive transport,” Alexandre says.
In the paper, the researchers present a new model of flow and transport in porous media that separates mechanical and diffusive mixing. The model combines the foundational larger-scale continuity equation with a stochastic momentum conservation equation that captures the randomness of flow due to the complex pore geometry of natural media. That’s mated with an advection-diffusion equation.
“We describe these two processes explicitly,” Alexandre says. The advection-diffusion equation describes random Brownian diffusion that occurs at the molecular scale, and the stochastic equation captures mechanical spreading due to random velocity variation on a larger scale.
The stochastic equation, in effect, injects random fluctuations to represent the variable flow velocity that occurs at scales too small for the model to capture. The noise also helps account for simplifying assumptions and for deviations from the smooth flow paths predicted by the continuity equations.
The injected fluctuations need not always be “white,” or uncorrelated, Alexandre says. “That’s where you start when you don’t have any information. You assume there is no correlation, but if you know more about your system you can try to use data tailored to the model.”
In the paper, the researchers compared their stochastic model against the standard deterministic model for three transport problems.
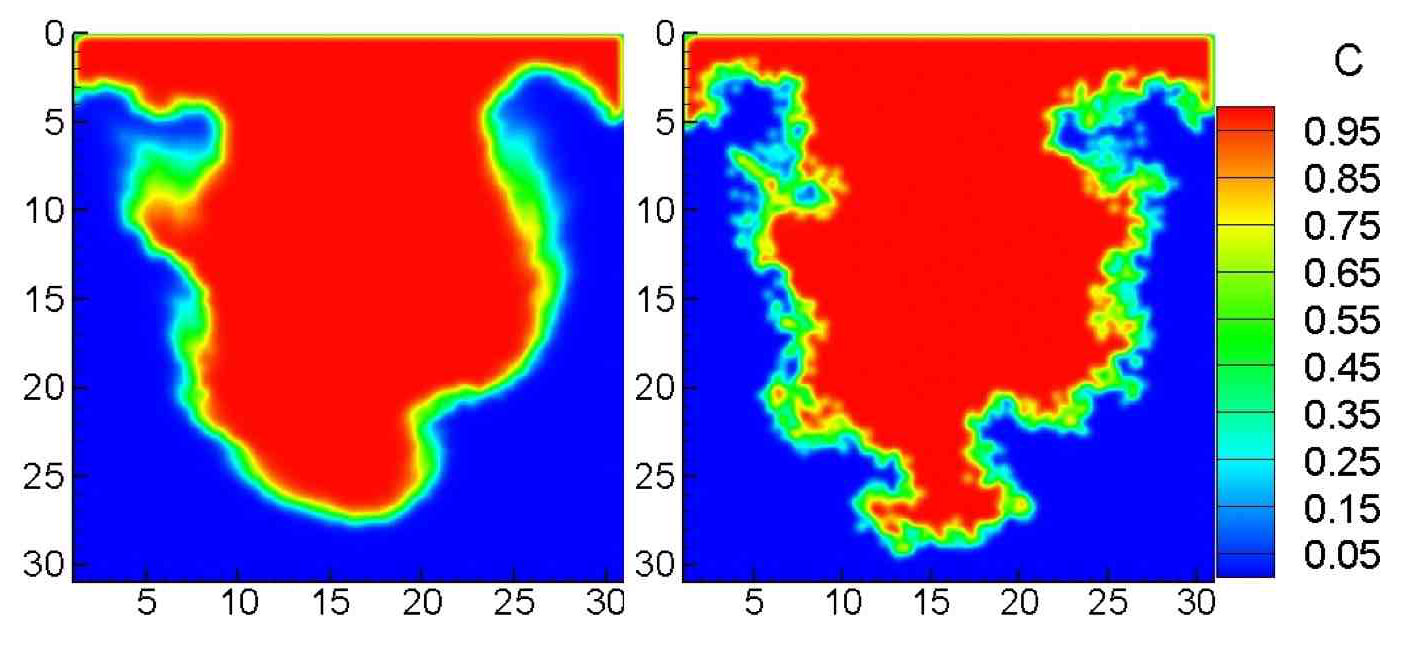
The first example tracked transport of a nonreactive tracer in a two-dimensional domain. The standard ADE model produced a well-mixed Gaussian (smoothly distributed) plume migrating through a homogeneous porous medium. In a visualization, it produces “a very smooth, kind of bell-shaped distribution of concentration,” Alexandre says.
The researchers’ stochastic model, in contrast, predicts non-uniform mixing similar to that found in experiments. “It’s very heterogeneous and will become Gaussian only if you average concentration over a certain volume,” Alexandre says. “If you are interested in some highly localized processes then the two models give very different results.”
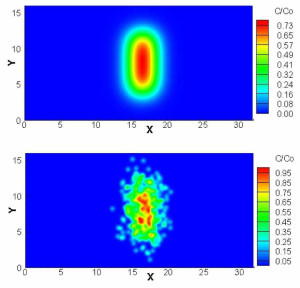
Deterministic (top) and stochastic (bottom) predictions of the concentration (C) of the reaction product C.
The second example modeled two solutes, A and B, which react to produce a third substance, C. The standard deterministic model predicts a mixing flow that widens uniformly in the flow direction, with concentrations of C varying smoothly within the mixing zone. A visualization shows a smooth, pointed profile as the reaction progresses.
The visualization of the stochastic model, however, is blurry, showing a non-uniform distribution of the reaction product. “The amount of C we obtain is very different,” Alexandre says, with the deterministic model overestimating the maximum concentration of C by an order of magnitude.
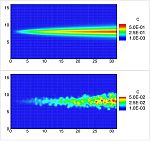
The last example modeled a Rayleigh-Taylor instability, or the displacement of a less-dense fluid by a more-dense fluid, as when a layer of brine displaces fresh water underneath it. The deterministic model predicts an interface between the fluids that is less complex than the stochastic model’s prediction.
The standard model “tends to over-smooth everything and it also smoothes the interface and makes it less rough. The stochastic model doesn’t smooth as much,” Alexandre adds.
The paper resulted from three different ASCR-supported projects, Alexandre says. One, backed by the Scientific Discovery through Advanced Computing (SciDAC) program, deals with subsurface reactive transport. Another looked at multiscale phenomenon, including subsurface flows. The third focuses on stochastic partial differential equations like those used in the PRL model.
The model is important for devising ways to remediate subsurface contamination, including radionuclides. In one approach, a chemical would be injected into groundwater to react with and immobilize the contaminants or to reduce them to less volatile form.
“We think that standard models can overestimate the amount of reaction,” Alexandre says, “so they can overestimate the effect of remediation. Our model will give a more accurate prediction of what is going to happen during remediation. If we have more accurate models we can design more effective remediation.”
The stochastic model still makes a number of assumptions that affect the quality of its predictions. It’s not based on “first principles,” where every equation is grounded in fundamental laws of physics. “We showed that this model does indeed qualitatively reproduce behavior one would see in experiments,” Alexandre says. “Our ongoing research aims to justify our model by deriving it strictly from the first principles.”
Assumptions and lack of data about real-world subsurface flows are among the factors contributing to model and parametric uncertainties, Daniel says. Another part of the research he shares with his brother seeks to put a number on uncertainty, using subsurface flows as a test bed.
It’s not just whether the equations provide an answer that fits available data, but whether they’re the right equations to start with and whether they rely on appropriate parameters. And just because a model fits available data doesn’t mean it will accurately predict system behavior in areas or regimes where data isn’t available.
At an October 2008 meeting of ASCR applied mathematics researchers at Argonne National Laboratory, Daniel described one approach: using small-scale models of subsurface flows to root out uncertainty in coarse-grained models. One example, investigated with Los Alamos National Laboratory researchers Gowri Srinivasan and Bruce Robinson, focuses on subsurface migration of ions of neptunium, a radioactive metal, in groundwater.
Neptunium ions can attach themselves to the solid matrix they pass through. “Obviously, if all of it attaches to the soil there will be nothing in the water,” Daniel says. “There will be no neptunium and everything is very nice and hunky dory. But you know that what attaches itself can eventually detach itself. All these things are described by equations and parameters” that contribute to uncertainty.
The project is progressing and the group’s techniques have addressed a few of the many uncertainties inherent in such models. Future research will focus on making the researchers’ uncertainty quantification techniques less computationally demanding.
Like the researchers’ method for modeling flow and transport, the techniques they’re developing also have broad potential for assessing uncertainty in a range of models, including nuclear reactors, cells and climate.
It’s no wonder, because uncertainty is everywhere. Says Daniel, “You can wish it away or pretend it’s not there, but it is.”