Cynthia Phillips looks at mundane things like packing a bag or driving across town differently than most people.
To her, they represent questions of optimization – problems that seek to maximize or minimize desired quantities or qualities. That means finding the best solution from among a myriad of possible combinations.
“Everyone makes decisions that could be thought of as optimization problems,” says Phillips, an applied mathematician and distinguished technical staff member at the Department of Energy’s Sandia National Laboratory in New Mexico.
For instance, “People who pack moving vans do a fantastic job with a very difficult geometric optimization problem,” Phillips says. “That’s very hard for computers to do.”
Phillips and her fellow researchers are out to make those kinds of jobs easier for computers – and the people who use them. They devise algorithms that let computers solve optimization problems quickly and efficiently.
Those problems are far thornier than finding the best ways to make deliveries or schedule workers.
“People can understand the complexities of dealing with (optimization) on an individual basis, and therefore can appreciate the difficulty of trying to do it for tens of thousands of objects that are all competing for resources,” Phillips says.
The algorithms Phillips and her fellow researchers devise or combine have broad uses, including:
- Determining the best spots to place sensors to detect water contamination.
- Finding the best routes to securely move nuclear materials.
- Choosing the best places to locate guards, cameras and sensors to detect intruders.
- How to place and manage wireless sensors for monitoring environmental conditions or numbers of endangered animals.
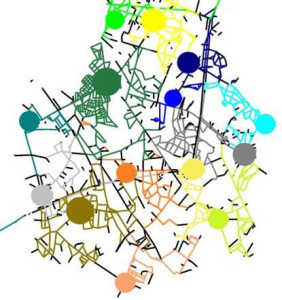
This shows how placement can optimize the effectiveness of a sensor network. Each colored dot is a sensor, and the portion of the network it “guards” – the part where it is the first sensor to detect an event – is the same color. The dot is sized in proportion to the number of contamination events the sensor is the first to see out of a set of “interesting” ones.
Every example is a complicated problem. It may include multiple variables and multiple limits, called constraints, on the solution – factors such as time, location and other conditions that must be satisfied in concert with the quantities or qualities to be maximized or minimized.
Phillips and other applied mathematicians call the set of possible solutions “search spaces” – and while they aren’t infinite, search spaces often are enormous.
“People talk about search spaces that contain more potential solutions than the number of atoms in the universe,” Phillips says.
“You have to be very intelligent about how you approach the question, or it’s hopeless,” Phillips says. Testing each solution isn’t practical or feasible. Instead, the algorithms she and her colleagues use exploit the structure of the problem to quickly find the right solution “region.”
Phillips often cites as an example a plan to place sensors in a city to detect some kind of contamination.
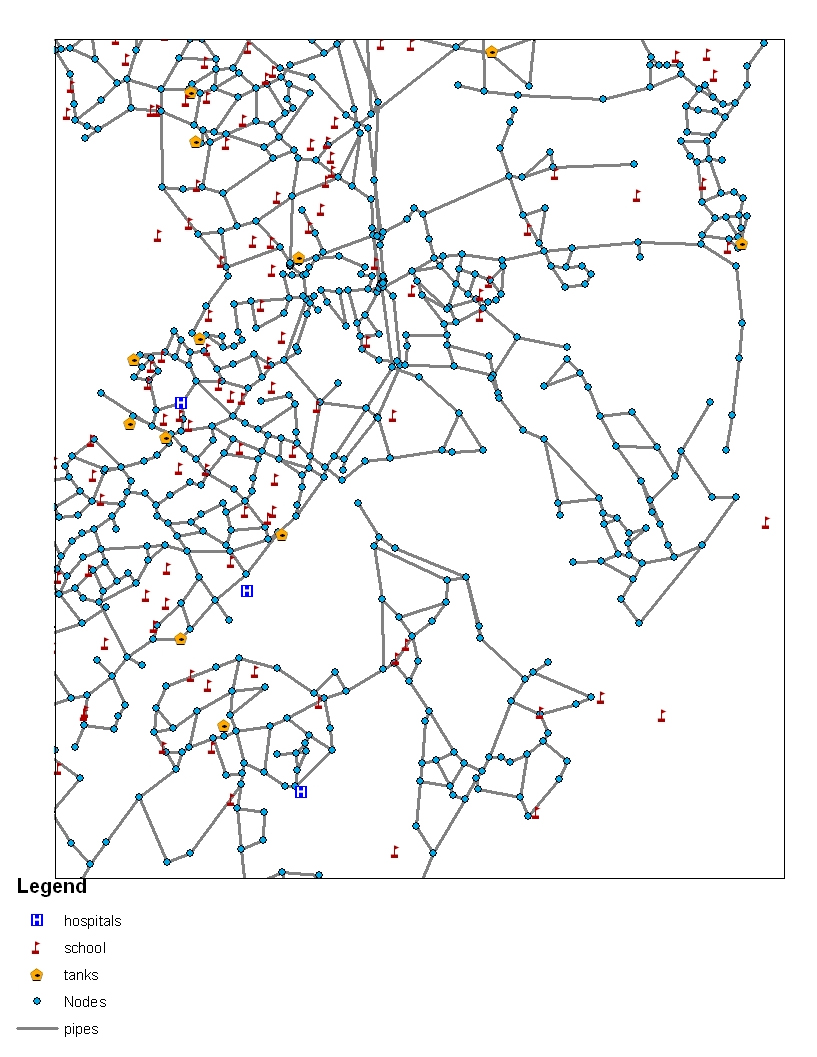
Optimization algorithms can help with complex problems like determining the best locations for sensors designed to detect water contamination. This image shows possible places a water utility might locate sensors on its system, such as publicly owned buildings.
“If we were considering 50,000 locations in a city for putting down my sensors and I have 200 sensors,” it would be impossible to test every combination of 200 to find the best, Phillips says.
But with discrete optimization, “I know something about that space of feasible solutions geometrically, algebraically or mathematically that allows me to ignore a lot of points I know aren’t going to be interesting,” Phillips says.
For instance, if the goal is to minimize a targeted value, it’s possible to run simple calculations and get a quick possible value for it – a value of 800, for example.
With that in hand, algorithms can test regions of the solution space to see if a better possible solution exists there. In the example, if the region holds no better solution than a value of 1,000, “Well, I already have something that’s better than that” – that value of 800, Phillips says. “I know I can throw everything out of the region without looking in detail at what’s in there.
Even with algorithms that limit the possible solutions, high-performance parallel computers – ones that break tasks up into many pieces so multiple processors can work on them for faster results – still are necessary to solve many optimization problems. Phillips and her researchers are designing algorithms that take advantage of that power.
“Parallel computers allow you to solve problems that can’t be solved” by other means, she adds. “If there’s a problem where the difference between an approximation and an optimal solution has serious consequences for the cost to the government, or for national security, if you’re willing to put in the time and the effort to run this on a big machine, that’s what our (computer) code is for.”
The techniques Phillips and her fellow researchers have developed can even improve the performance of parallel computers themselves.
Large parallel machines with thousands of processors often have several jobs running at one time, Phillips says. “Each job might be allocated to some subset of processors, and it could be that having those jobs close to each other is important in terms of not having their communication interfere with others, and having fast response to their own communication,” she adds.
Phillips’ group created the Compute Processor Allocator (CPA) to parcel out processor nodes based on location and to balance job allocation with future allocations on large computers. In experiments, CPA increased locality and processor production on a parallel computer by 23 percent over other allocators.
The program earned an R&D 100 Award as one of the top new technologies of 2006.
Now Phillips and her fellow researchers are working with computer scientist Ali Pinar of the DOE’s Lawrence Berkeley National Laboratory on the “Supernova Factory Scheduler,” a program designed to maximize telescope time to find and monitor exploding stars.
Other new applications include tracking particle movements in supercolliding “atom-smashers” and detecting groundwater contamination.
In fact, Phillips says, there are so many uses for optimization codes that “I sometimes refer to our group as mathematical mercenaries, since we can usually find applications to work on” regardless of circumstances.
