What University of California at Los Angeles mathematician Russel Caflisch does is like trying to grab a handful of fire. Caflisch is creating computer simulations of plasmas – clouds of ionized gas sometimes referred to as the fourth state of matter.

Plasmas are in neon lights and lightning.  High-temperature plasmas are at the heart of stars – and of proposed nuclear fusion reactors, touted as clean energy sources for the future.

Computer simulations are critical to developing fusion because high-temperature plasmas are difficult to measure experimentally.  Reactions take place in millionths of a second, at temperatures in the millions of degrees – much too high for most instruments.

With simulations, “You can see everything that’s going on,” Caflisch says.  “You can slow it down artificially and you also can test things you wouldn’t be able to easily test experimentally.”

Simulations also can cost orders of magnitude less than experiments, he adds.

But computer simulations often run too slowly and produce unreliable results.  “You’ll see that even today,” Caflisch says.  “Two different simulations might give quite different results.”

To change that, Caflisch and his fellow researchers must bridge huge spans of space and time.  They must combine mathematical methods depicting the tiniest particles with those depicting whole plasma clouds.

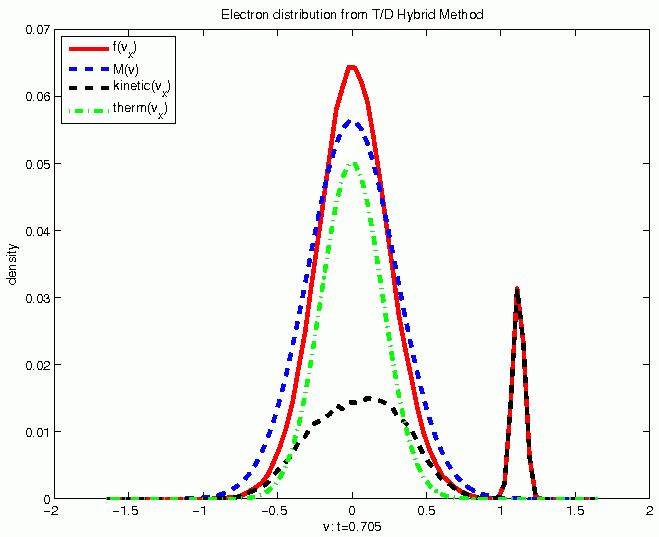
This graph shows the velocity distribution of electrons in a plasma as simulated with a hybrid method (red line), which combines an approach depicting the cloud as a thermalized fluid (green line) with a kinetic approach characterizing it as discrete particles (black line). Note the “spike” centered around v≈1.1; it corresponds to a known real-world effect called a “bump-on-tail”, and is almost entirely a contribution from the kinetic part of the calculation. A distribution based solely on fluid flow equations is shown in blue for comparison.

Caflisch and fellow researchers from the Department of Energy’s Lawrence Livermore National Laboratory started with one important aspect of plasma simulation: Modeling collisions of ions – electrically charged atoms and molecules – and electrons.

“One of the most challenging problems in the simulation is to take those into account,” he adds.  Simulating billions of collisions can slow computation to a crawl.

It’s faster to depict the particles as fluid elements, with each element containing millions of particles.  “The trouble is the fluid equations aren’t quite accurate there,” Caflisch says. “We’re trying to blend those two together to get the speed of the fluid part and the accuracy of the particle part.”

Plasmas are difficult because the electrical charges of ions and electrons interact.

To model particles, Caflisch uses the Monte Carlo method, so named because it relies on random numbers.

“We’re starting with a system that has maybe 10²⁰ particles in it, which is a huge number” – a one followed by 20 zeroes, Caflisch says.  “We’re trying to model it with 10,000 or 1 million particles.

“The way we do that is by randomizing the interactions so each numerical interaction represents millions of real interactions.  That works amazingly well.”

Caflisch and his fellow researchers combine that with a fluid model.

“You represent the billions of particles by thinking of them as forming a collective unit that moves with a fluid speed and pressure and such,” Caflisch says.

The model evolves those properties through space and time as particles are selected out of the fluid distribution.  The particles, in turn, influence the density, momentum or energy of the fluid.

Caflisch and his fellow researchers didn’t start out cold when they began work to simulate hot plasmas. They’d successfully used their multiscale mathematics approach before, to model rarefied gas flow in the upper atmosphere.  Plasmas are more difficult, however, because the electrical charges of the ions and electrons also interact.

Caflisch says his algorithms – mathematical recipes – could model other phenomena, such as interactions of air with the read-write heads on computer disc drives.  Air must pass under the head to keep it floating just microns above the disc surface.

“It’s like oil in a car,” Caflisch says.  “The way that flows is rather similar, from our point of view, to what’s happening in these rarefied gas flows and in plasma flows.”

Caflisch says the many applications of his work fascinate him.

“What I love the most is the chance to work with scientists and engineers and learn about the technology they’re doing, and to contribute something to that,” he adds.