Nobody would use a buzz saw to carve a toothpick. Nor would a sensible person use a crowbar to open a sardine can.
It takes the right tool in the right situation to get the job done quickly and efficiently.
Computational scientists face similar issues: When is a particular mathematical tool right for a particular simulation of a physical phenomenon?
Bill Henshaw helps answer that question. He designs and combines algorithms – mathematical recipes – that computers use to simulate things like ice accumulation on airplane wings, cooling nuclear reactors – even how a bomb explodes.
Most such simulations involve moving geometry – objects moving through space and interacting with fluids and other objects.
“That’s a very difficult problem for many computational people,” says Henshaw, an applied mathematician at the Department of Energy’s Lawrence Livermore National Laboratory in California.
For convenience or simplicity, researchers sometimes use a single technique – a single tool – to attack such problems. That’s not always the best choice, Henshaw says, because as the object or area being modeled changes, the technique is less effective. It’s a bit like using a chainsaw to cut down an oak tree, then using the same saw to carve intricate designs on an eggcup made from the oak.
Henshaw’s research combines tools that automatically adapt to use the best ones for specific parts of the simulation. Different algorithms “behave better in different regimes, so you want to use the appropriate algorithm” where it’s most effective, he adds.
The closer together the points are, the more precise the model is – and the more computer power it demands.
“Part of what I do is try to look at the existing good algorithms out there, design new ones that actually form composite or hybrid methods,” and apply them to complex problems, Henshaw says.
That’s the approach behind Overture, a set of tools Henshaw’s group developed to simulate physical phenomena such as fluid dynamics – the movement of liquids or gases, like water through a pipe or air over a car – , combustion and electromagnetics. Overture adapts the algorithm as the problem changes shape.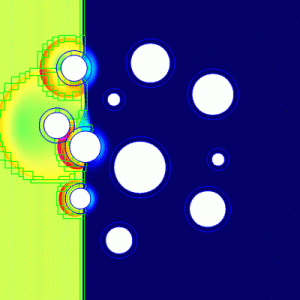
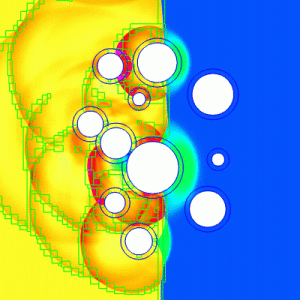
Computation of a shock, moving from left to right and hitting a collection of cylinders immersed in a gas through which the shock passes; color denotes density, which is shown at two different times. This computation illustrates the use of moving grids and adaptive mesh refinement (AMR). Each cylinder is treated as a rigid body that moves according to the forces exerted by the fluid. The boundaries of the curvilinear grids are shown in blue. The boundaries of the AMR grids are shown in green.
It’s in the formulas
Complex formulas called partial differential equations (PDEs) mathematically describe the continuous processes, like combustion, that Henshaw’s tools model. PDEs are the core of many simulations, but computers can’t solve them until the PDEs are approximated by algebraic equations at discrete data points.
The data points are distributed in a grid or mesh pattern throughout the area in which a process, such as fluid flow, is being modeled. The computer calculates what’s happening to pressure, velocity, temperature and other properties at each one of the data points as the simulation progresses.
Taken together, the points portray what’s happening. The closer together the points are, the more precise the model is – and the more computer power it demands.
The right mesh or grid is critical to finding a solution quickly and accurately, Henshaw says.
“You want that to have very nice properties, because it makes the rest of your problem easier,” he adds. But as problems change, such as when modeling moving objects, “then this fundamental structure has to change; this grid has to change.”
For some solution techniques, changing creates big demands for computer resources, Henshaw says. The computer must regenerate the grids while retaining all the right properties, such as well-distributed data points. In some cases, the grids may become tangled.
In other methods, the algorithm may be precise and fast, but may require time and resources to start. Restructuring the grid means reinitializing the problem, which causes delays and demands resources, Henshaw says.
“You need to have methods that have low startup. … The job is to come up with algorithms that allow you to do that,” Henshaw says. For instance, his group’s methods keep high-quality grids, but change them only where needed to capture important phenomena, like at the boundary between an object and the shock wave or fluid encountering it.
“The approaches we use are very efficient at both allowing you to rapidly change the geometry, but also to keep a nice underlying structure,” he adds.

This animation shows a simulation of a shock wave moving through a gas and pushing cylinders. Eventually the shock wave reflects off the wall at the right and hits the cylinders again. The simulation also generates reflected shocks, with colors showing different gas densities. “Cool” colors such as blue correspond to low densities, while “hot” colors such as red and pink depict high densities. The computer represents density as values located at approximately 1 million discrete “grid points” distributed throughout the space being modeled. The number and position of these discrete values changes over time. The black boxes show grid boundaries, which are sub-regions in the space being modeled where grid points are moving or where the number of points has been increased to obtain a more accurate answer.
Connecting to the grid
For instance, Henshaw and his fellow researchers developed a method that applies rectangle-shaped Cartesian grids throughout most of an area being modeled. Cartesian grids are simple and efficient, but difficult to use on complex geometries, like flow over an airplane’s surface. So, Henshaw’s methods use composite or overlapping grids in parts of the domain modeling those complex geometries.
“We’ll use Cartesian grids away from the boundaries, where you can take advantage of the very efficient representation,” Henshaw says. “You can come up with algorithms that are as efficient as methods used for Cartesian grids, but you also get the higher accuracy at boundaries.”
Many of these methods are packaged into the Overture toolkit. Henshaw and his fellow researchers have used them on projects ranging from modeling coolant flow in the next generation of high-temperature nuclear reactors to simulating ice buildup on airplane wings.
One of the more unusual applications, however, is modeling what happens when a bomb goes off.
“Even though people are very good at designing them, they don’t really understand a lot of the basic properties of explosives,” Henshaw says. “They don’t really understand exactly when you set off the explosive, how the initial phase works. … Unless you can understand that, it’s hard to design explosives with new properties.”
Modeling an explosion is, as you might guess, quite tricky. The boundary between burnt and unburnt material – the place where the explosive energy is generated – is exceedingly small and moves exceedingly fast.
“There’s a lot of detailed structure in that very narrow region, so you have to have a good method that can represent that,” Henshaw says.
It’s the kind of challenge he loves. Although Henshaw is a mathematician working on algorithms, his favorite part is seeing the results.
“You can understand a certain amount by analyzing the equations, but you understand another part by actually doing simulations and seeing things that you couldn’t initially see,” he adds. “I like that combination.”