For Darryl Holm, it’s about the geometry.
Holm, an applied mathematics professor at London’s Imperial College, studies how shape affects complex systems. The mathematics of how things fit together has governed his work, from climate modeling to imaging science.
Now he’s focused on nanosensors – molecules formed into tiny shapes thousands of times thinner than a hair, but potentially capable of detecting substances in minuscule amounts.
Holm’s work breaks new ground in understanding how these nanosensors self-assemble. It’s part of a continuing collaboration with researchers in the United States. In fact, he’s still a fellow at Los Alamos National Laboratory, a U.S. Department of Energy facility where he worked for more than 30 years.
Nanoscale science holds the promise of tiny, fast computers and other devices. That potential – and the obstacles to it – depends on how molecules behave at such small scales.
Holm and his colleagues wanted to model the basic principles that underlie both how individual molecules come together to form a simple nanosensor and how the molecules’ geometry affects that process.
Holm is extending the mathematics behind nanosensor construction in new directions.
Holm and Vakhtang Putkaradze at Colorado State University modeled construction of a nanosensor just 1 centimeter long, but containing roughly 10 trillion molecules. The string of molecules can conduct electricity. If a molecule of the substance being detected binds to the sensor, the circuit breaks, indicating the presence of the target substance.
To build such sensors, nanoscientists, such as those at the Center for High Technology Materials at the University of New Mexico, first apply the sensor molecules to a template – a groove etched into a surface.
But the molecules “won’t stay in the grooves because they’re quantum things. They hop around and they have something like Brownian motion (the random motion of small particles suspended in a gas or liquid) going for them if they have any temperature,” Holm says. To get them to stay in place, “you paint something that is going to shrink across them, and you want that shrinkage to force them into the little grooves and line them up.”
Holm wants to know how this “shrink wrapping” works on the molecular scale. The small motions of the molecules compete with the larger scale external force that forms the line, pushing the molecules closer to each other.
As the molecules converge, their shape will affect if and how they will clump. If they clump together, or aggregate, in a straight line, the mathematical model will produce a singularity representing the desired concentration of molecules along a line.
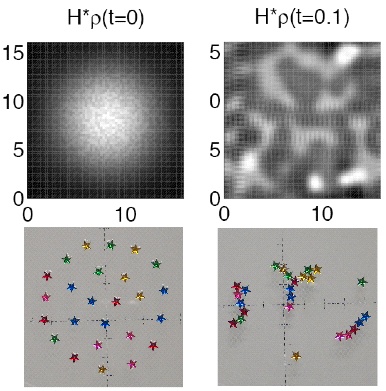
Objects floating in water mimic the forces used in assembling sensors on the nanoscale: An experiment, conducted by P. D. Weidman (U Colorado), used 4mm plastic floating stars distributed and oriented randomly within a circular shape (bottom left). After being carefully lowered onto the water’s surface to avoid convection, the stars assembled into lines or branched tree-like structures within an hour (bottom right). Although the positioning of the groupings on the surface is random, calculations using Holm and Putkaradze’s model reproduce the typical shapes found in the experiment (top right).
Understanding how molecules’ shape determines the patterns into which they aggregate gives nanoscientists a valuable tool as they design their experiments.
For example, circularly symmetric molecules in a plane will aggregate into patches, like Cheerios floating in milk. Star-shaped molecules will aggregate into branched structures that nanoprocessing techniques can force into linear patterns.
Holm is extending the mathematics behind nanosensor construction in new directions. Traditionally, mathematicians want to avoid singularities, he notes, because in many systems, they can indicate a problem in the original definition of a system or that the solution has broken down.
In this system, however, the mathematical singularity describes how the molecules are self-assembling, and the researchers are forced to examine these solutions further to tease out the mechanisms.
“We need this kind of solution in order to describe these nanoprocesses,” Holm says. “And moreover we need to find the dynamics of these solutions, how they form, where they form, what their time dependence is and what happens after they form, because you may want to still move them and find out how they interact with each other.”
Holm’s work is extending applied mathematics by challenging conventional wisdom, an attitude he traces to his childhood.
“Sputnik happened the day I turned 10,” he says, and he and other gifted students in Minneapolis were launched into an accelerated and enriched math and science program.
When Holm was 13, an after-class discussion with his higher algebra teacher led him to stay up late, finding his own approaches to problems.
“What I discovered sometime in the middle of the night was that mathematics is a power that allows you to make your own rules,” Holm says. “As long as your rules are consistent and you can explain them, no one can arbitrarily say they aren’t right. As a kid, I was thrilled about creating new rules and seeing where they led. And that’s the path I’ve always followed.”